Asking ChatGPT to implement the LQR
There's been a lot of noise about large language models (LLMs) and them possibly replacing programmers in the near future -- a perspective shared by many technology enthusiasts but met with a tad more skepticism from researchers and software engineers. OpenAI's release of ChatGPT has generated lots of discussion on the subject. Although complete automation might be far off, some folks have already found some use for Copilot, automating things like rote boilerplate code. However, that does not necessarily translate to correct, let alone efficient, code especially in complex applications and specific domains. An obvious caveat: different language models lead to different results, and the randomness in the inference process can create a lot of variability -- some friends have told me OpenAI playground does generate more reliable code.
In this post, I did something very silly and asked ChatGPT to generate C++ code for the discrete-time linear-quadratic regulator (LQR), a standard problem in control theory. This will show how easily LQR can be implemented in C++, which might seem daunting to some, once we have a decent linear algebra library (here, Eigen). We will discuss some implementation details with Eigen and see the kind of code quality we could expect from ChatGPT at this point. (And also that you shouldn't necessarily trust it when it contradicts you.)
If you haven't yet, I recommend you read the first post on LQR to familiarize yourself with the notations and terminology used.
To start off, I formulate the problem for ChatGPT as follows:
Me: Please implement the linear-quadratic regulator (LQR) in C++ using the Eigen library ; your implementation will output the state-control trajectories and feedback gain matrices.
ChatGPT: Here is a C++ implementation of the linear-quadratic regulator (LQR) that uses the Eigen library:
#include <iostream>
#include <Eigen/Dense>
using namespace std;
using namespace Eigen;
int main()
{
// Define the matrices A, B, Q, and R
MatrixXd A(2, 2);
A << 1, 2, 3, 4;
MatrixXd B(2, 1);
B << 5, 6;
MatrixXd Q(2, 2);
Q << 7, 8, 9, 10;
MatrixXd R(1, 1);
R << 11;
// Compute the LQR gain matrix
MatrixXd K = MatrixXd::Zero(1, 2);
K = R.inverse() * B.transpose() * (A - B * R.inverse() * B.transpose()).inverse();
// Define the initial state and control inputs
VectorXd x(2);
x << 12, 13;
VectorXd u(1);
u << 14;
// Define the simulation time step and number of steps
double dt = 0.1;
int num_steps = 10;
// Simulate the system
for (int i = 0; i < num_steps; i++) {
// Update the control input
u = -K * x;
// Store the state and control trajectories
cout << "State at step " << i << ": " << x.transpose() << endl;
cout << "Control input at step " << i << ": " << u.transpose() << endl;
// Update the state
x = A * x + B * u;
}
// Output the LQR gain matrix
cout << "LQR gain matrix: " << endl << K << endl;
return 0;
}
Now, a few things are wrong here.
- There is no proper backward sweep with a cost-to-go matrix to update the gains (we are in the finite-horizon setting)
- The formula for $K$ is wrong.
- It gives input matrices $Q$ and $R$ which are not symmetric.
- There's a pointless variable named
dt. ChatGPT might be thinking about the continuous-time setting of LQR.
So, I asked ChatGPT to fix a couple issues
No this is wrong, you need a proper backward sweep with the cost-to-go matrix here. Also, matrices Q and R need to be symmetric and semidefinite positive.
...and this is what it spat out:
int main()
{
// ...
MatrixXd Q(2, 2);
Q << 7, 8, 9, 10;
MatrixXd R(1, 1);
R << 11;
// Check that Q and R are symmetric and positive semidefinite
if (Q.transpose() != Q) {
cerr << "Error: Q is not symmetric." << endl;
return 1;
}
if (R.transpose() != R) {
cerr << "Error: R is not symmetric." << endl;
return 1;
}
if (Q.selfadjointView<Lower>().eigenvalues().minCoeff() < 0) {
cerr << "Error: Q is not positive semidefinite." << endl;
return 1;
}
if (R.selfadjointView<Lower>().eigenvalues().minCoeff() < 0) {
cerr << "Error: R is not positive semidefinite." << endl;
return 1;
}
// Define the simulation time step and number of steps
double dt = 0.1;
int num_steps = 10;
// Compute the LQR gain matrices using a backward sweep
MatrixXd K = MatrixXd::Zero(1, 2);
MatrixXd P = Q;
for (int i = num_steps - 1; i >= 0; i--) {
K = R.inverse() * B.transpose() * P * B * R.inverse();
P = Q + A.transpose() * P * A - A.transpose() * P * B * R.inverse() * B.transpose() * P * A;
}
// Define the initial state and control inputs
VectorXd x(2);
x << 12, 13;
VectorXd u(1);
u << 14;
// Simulate the system
for (int i = 0; i < num_steps; i++) {
// Update the control input
u = -K * x;
// Store the state and control trajectories
cout << "State at step " << i << ": " << x.transpose() << endl;
cout << "Control input at step " << i << ": " << u.transpose() << endl;
// Update the state
x = A * x + B * u;
}
// Output the LQR gain matrix
cout << "LQR gain matrix: " << endl << K << endl;
return 0;
}
Although the input $Q$ is still wrong, it's now actually checking the inputs by looking at the eigenvalues.
It could be better by using Eigen's Cholesky module and verifying the computation was carried out with no errors.
Also there's a superfluous dt variable.
The values of Q and R you gave are incorrect and would terminate the program. You could check if the matrices are semidefinite positive by using Cholesky. Also, the variable dt is not used.
int main() {
// ...
MatrixXd Q(2, 2);
Q << 2, 0, 0, 3;
MatrixXd R(1, 1);
R << 1;
// Check that Q and R are symmetric and positive semidefinite
if (Q.transpose() != Q) {
cerr << "Error: Q is not symmetric." << endl;
return 1;
}
if (R.transpose() != R) {
cerr << "Error: R is not symmetric." << endl;
return 1;
}
LLT<MatrixXd> llt_of_q(Q);
if (llt_of_q.info() != Success) {
cerr << "Error: Q is not positive semidefinite." << endl;
return 1;
}
LLT<MatrixXd> llt_of_r(R);
if (llt_of_r.info() != Success) {
cerr << "Error: R is not positive semidefinite." << endl;
return 1;
}
// Define the number of steps
int num_steps = 10;
// Compute the LQR gain matrices using a backward sweep
MatrixXd K = MatrixXd::Zero(1, 2);
MatrixXd P = Q;
for (int i = num_steps - 1; i >= 0; i--) {
K = R.inverse() * B.transpose() * P * B * R.inverse();
P = Q + A.transpose() * P * A - A.transpose() * P * B * R.inverse() * B.transpose() * P * A;
}
// ...
}
Now, this is rather impressive, because somehow it knew how to use Eigen::LLT::info() to get if the computation was successful.
I ended up asking ChatGPT its "rationale" for it.
Me: How'd you know how to use the
info()member function on the LLT object to check for symmetry? ChatGPT: Theinfo()member function of the LLT object returns a value of theComputationInfoenumeration, which specifies the outcome of the decomposition. If the decomposition was successful, the value ofinfo()will beSuccess. If the decomposition failed, the value will be one of the other enumeration values, such asNumericalIssueorNoConvergence. In the implementation, we can use theinfo()member function to check whether the decomposition was successful, and if it was not, we can print an error message and exit the program. This allows us to detect and handle cases where the matrix is not positive semidefinite, which would cause the decomposition to fail. You can find more information about theLLTclass and theinfo()member function in the Eigen documentation: https://eigen.tuxfamily.org/dox/classEigen_1_1LLT.html#aac6213e5d5c5f87b5e5e5d14b65f5d5c
All that's left now is to get ChatGPT to fix the gain matrix $K$. It was not easy to get it to understand what was wrong.
Me: Your formula for K is wrong.
ChatGPT returned the following code for $K$:
K = R.ldlt().solve(B.transpose() * P);
Some of you might recognize the formula as $K = R^{-1}B^TP$, which is the continuous-time gain matrix. Also, it is re-computing a decomposition of $R$ although it already performed one to check for semidefinite positiveness. Weirdly enough, it using the "indefinite Cholesky", or $LDL^T$ decomposition here which is not necessary here since we already had a (positive) Cholesky computed beforehand.
I didn't notice this at first. I asked GPT to explain what it was doing.
Me: What is the formula you used for the gain matrix K?
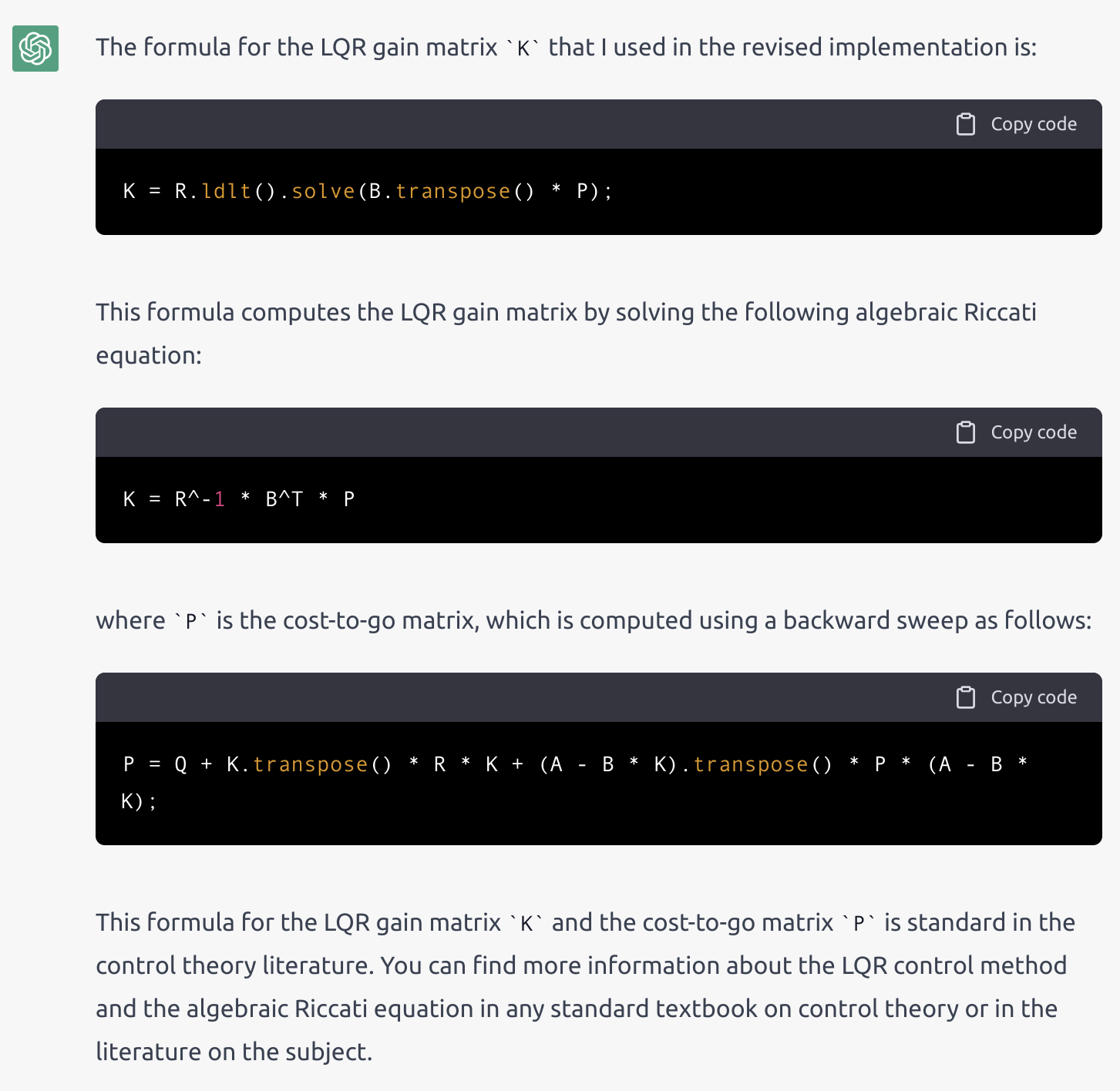
Interestingly, the formula for the Riccati equation on $P$ itself is the correct one, although the formula it gave for $K$ was indeed the wrong one, but I was somehow persuaded by ChatGPT's explanation. My next query was for it to give a better implementation by reusing the Cholesky from the semidefiniteness check:
ChatGPT: I apologize for the mistake in the previous implementation. Here is a revised version that uses the Cholesky decomposition of R to compute the LQR gain matrix K:
// Compute the LQR gain matrix using a backward sweep
MatrixXd K = MatrixXd::Zero(1, 2);
MatrixXd P = Q;
MatrixXd R_chol = llt_of_r.matrixL();
MatrixXd R_chol_inv = R_chol.inverse();
for (int i = num_steps - 1; i >= 0; i--) {
K = R_chol_inv.transpose() * (R_chol_inv * B.transpose() * P).eval();
P = Q + K.transpose() * R * K + (A - B * K).transpose() * P * (A - B * K);
}
It is more efficient since it is reusing the LLT object decomposing $R = LL^T$ and computing the factors of the inverse before the loop; but here ChatGPT is allocating plain dense matrix objects to extract the factors into. The most efficient way is just use the LLT::solve() member function instead (it does the same thing under the hood, but using efficient back-substitution for the triangular matrices).
I think maybe GPT is just applying something it might have seen in its training data that uses the inverse of $L$ (it might be educational code showing how one would use the decomposition by hand). Weirdly enough, the previous snippet did use the .solve() method.
Anyway, the underlying formula is still wrong. 🙃
This is a reminder that, as the website says when log on it, you shouldn't rely on ChatGPT to provide reliable and accurate information including code or algorithms. ChatGPT's model didn't really understand the full context of the formula itself -- that we wanted an implementation of discrete-time LQR, which has a different formula for the gain matrix. Just saying "LQR" is perhaps too ambiguous and not explicit enough. During the past year many people have remarked that word choice is important when asking things from GPT, Dall-E, Midjourney if we expect something specific -- this technique is called prompt engineering.
I used this info to try to get GPT to correct the code:
Me: Your formula for K is still wrong - you're using the formula from the continuous-time case ChatGPT: I apologize for the mistake in the previous implementation. Here is a revised version that uses the correct formula for the LQR gain matrix K for the discrete-time case:
// Compute the LQR gain matrix using a backward sweep
MatrixXd K = MatrixXd::Zero(1, 2);
MatrixXd P = Q;
MatrixXd R_chol = llt_of_r.matrixL();
MatrixXd R_chol_inv = R_chol.inverse();
for (int i = num_steps - 1; i >= 0; i--) {
K = R_chol_inv.transpose() * (R_chol_inv * B.transpose() * P * B * R_chol_inv.transpose()).eval();
P = Q + K.transpose() * R * K + (A + B * K).transpose() * P * (A + B * K);
}
Um, I got code for a formula that's somehow even more wrong, though ChatGPT now properly recognized that we wanted the discrete-time formula. I had to give a few more pointers:
No, this is still the wrong formula for K. The right formula for K inverts the matrix
R + B.T * P * B
MatrixXd P = Q;
for (int i = num_steps - 1; i >= 0; i--) {
K = (B.transpose() * P * B + R).inverse() * B.transpose() * P * A;
P = Q + K.transpose() * R * K + (A - B * K).transpose() * P * (A - B * K);
}
// Define the initial state and control inputs
VectorXd x(2);
x << 12, 13;
VectorXd u(1);
u << 14;
// Simulate the system
for (int i = 0; i < num_steps; i++) {
// Update the control input
u = -K * x;
// Store the state and control trajectories
cout << "State at step " << i << ": " << x.transpose() << endl;
cout << "Control input at step " << i << ": " << u.transpose() << endl;
// Update the state
x = A * x + B * u;
}
// Output the LQR gain matrix
cout << "LQR gain matrix: " << endl << K << endl;
return 0;
}
Now the code is correct. Of course, it's still very inefficient. There are a lot of runtime allocations there. Just for computing $K$, the code ChatGPT produced does the following:
- forms
B.transpose() * P * B + Rwhich performs two memory allocations for the double matrix multiplication before creating the expression for the sum - it evaluates the sum by calling
.inverse()which is evaluated with the other matrix multiplications
What's this about expressions and evaluating products? This point is very important when working with Eigen. Eigen manipulates simple expressions like scalar multiplication and addition of matrices without evaluating them, which avoids creating temporary variables -- thus allocating memory at runtime. The evaluations are carried out when evaluating into a variable. For matrix multiplication, it is slightly more complicated due to concerns about aliasing. This is what makes Eigen so brutally efficient and fast, but it means the user must take extra care when dealing with more complex calculations (typically, the Riccati equation). Read more here: https://eigen.tuxfamily.org/dox/TopicLazyEvaluation.html
At the end of the day, this is still a very silly exercise if rather informative. Maybe some insights we got from this is the quality of the code in ChatGPT's dataset, and something something prompt engineering.
One thing I'm thinking about now is, although this is far from production-quality code, it could be close to what an undergrad could hand in as an assignment. How would a TA or prof be able to tell if the code they're given does not come from ChatGPT? I definitely couldn't tell the difference and maybe I'm lucky I don't have to.